Les exercices : oscillations libre RLC série
2 bac PC – SM - SVT
Exercice n°1
On charge totalement un condensateur de capacité C=45.3μF par un générateur idéal de f.é.m. E on le monte à une bobine d’inductance L et de résistance r à t=0. On visualise par un oscilloscope la courbe que représente la tension Uc(t) en fonction du temps.
1)Montrer comment relier l’oscilloscope pour visualiser la tension Uc (t).
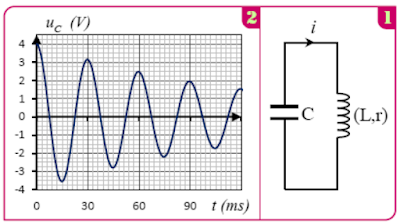
2)Quel est le régime observé ?
3)Quelle est la forme d’énergie stocké dans le circuit à t=60ms ? justifier.
4)En considérant la pseudo-période T est égale à la période propre T0 de l’oscillateur LC déterminer la valeur L.
5) Calculer ∆E la variation de l’énergie totale entre les instants t=0 et t1=90ms expliquer le résultat.
6)Trouver l’équation différentielle vérifiée par Uc (t).
7) On monte en série avec le condensateur et la bobine un générateur G délivrant une tension proportionnelle à l’intensité du courant UG=a.i et on obtient des oscillations sinusoïdales lorsque a=8 (SI)
- Quelle est le rôle du générateur G
- Déterminer l’équation vérifiée par la charge q dans ce cas.
8) Trouver r la résistance de la bobine.
Exercice n°2
On étudie le circuit idéal LC. Un groupe d’élèves ont chargés totalement le condensateur de capacité C sous une tension U puis ils ont montés le condensateur avec une bobine d’inductance L et de résistance négligeable.
1) Indiquer le régime observé.
2) Représenter dans la convention réceptrice les tensions Uc et UL.
3) Déterminer l’équation différentielle vérifiée par la tension Uc
4) La figure 2 représente les variations de Uc en fonction du temps .En exploitant la courbe écrire l’expression de la tension Uc (t).
5) L’énergie magnétique Em stockée dans la bobine varie en fonction du temps selon la courbe représentée dans la figure 3.
Montrer que l’énergie Em s’écrit :
En exploitant la courbe Em=f(t) déterminer la capacité C.
6-Trouver l’inductance L.
Exercice n°3
Pour connaitre l’effet de la résistance r d’une
bobine (b) sur l’énergie totale du circuit RLC ,un élève a
monté à t=0 un condensateur de capacité C=2,5µF initialement
changé avec la bobine. Par un dispositif adéquat on visualise les variations des
énergies Ee et Em en fonction du temps.
1) Indiquer le régime des
oscillations.
2) On suppose T=T0
déterminer la valeur de L.
3) Déterminer l’équation
différentielle vérifiée par q.
4)
L’énergie totale E= Ee+Em.
a) Exprimer l’énergie E en fonction de C ;L ;q et dq/dt.
b) Montrer que l’énergie totale diminue au cours du temps selon la relation
dE=-ri^2
dt![]() .
expliquer cette diminution.
.
expliquer cette diminution.
Exercice n°4
Un professeur de physique se propose dans un premier temps,
d’étudier l’influence de la résistance d’un conducteur ohmique sur la constante de temps au cours de
la charge d’un condensateur, et d’étudier dans un
deuxième temps, le circuit RLC dans
le cas d’un amortissement négligeable.
Pour cela, il demande à ses élèves de réaliser le montage schématisé
sur la figure 1 constitué de :
- Un générateur idéal de tension de force électromotrice E ;
- Un conducteur ohmique de résistance R réglable ;
- Un condensateur de capacité C ;
- Une bobine d’inductance L et de résistance négligeable ;
- Un interrupteur K à double position.
Après avoir chargé totalement le condensateur de capacité C =100μF , un élève bascule l’interrupteur K sur la position 2 ( voir Figure 1). La courbe de la figure 2 représente l’évolution temporelle de la charge q(t) du condensateur.
- Etablir l’équation différentielle vérifiée par la charge q(t).
- La solution de cette équation différentielle est : q(t)=Qm cos (2π/T0 t). Trouver en fonction de L et de C l’expression de la période propre T0 de l’oscillateur électrique.
- Vérifier que la valeur approximative de l’inductance de la bobine étudiée est : L ≈0,91H
- Calculer l’énergie totale du circuit aux instants t1=0 et t2=T0/4 Justifier le résultat obtenu.
Télécharger l'exercice 4 PDF : cliquer ici la correction cliquer ici